How to see generalized Stokes’ Theorem through Musical Isomorphism: Part 1

When I first encountered vector calculus, it felt incredibly daunting, especially trying to recall the three most crucial theorems: Green’s theorem, the Divergence theorem, and Stokes’ theorem. As years went by, I nearly forgot the material I had learned during my first year as a physics minor. After a long time, I decided to revisit it. However, this time, I approached it with a new perspective: through the lens of Differential Geometry. Let’s see what insights I can glean from that period.
Green’s Theorem: Let C be a positively oriented, piecewise smooth, simple closed curve in a plane, and let D be the region bounded by C. If L and M are functions of (x, y) defined on an open region containing D and have continuous partial derivatives there, then:

where the path of integration along C is anticlockwise.
Divergence Theorem: Suppose V is a subset of R³ which is compact and has a piecewise smooth boundary S (also indicated with ∂𝑉=𝑆). If F is a continuously differentiable vector field defined on a neighborhood of V, then:

The left side is a volume integral over the volume V, the right side is the surface integral over the boundary of the volume V.
Stokes’ Theorem: Let Σ be a smooth oriented surface in R³ with boundary ∂Σ≡Γ. If a vector field F,

is defined and has continuous first order partial derivatives in a region containing Σ, then:

If these don’t scare you, I don’t know what will! Now, before we bring all these theorems together, let’s define the types of n-surfaces in R³. A 0, 1, 2, and 3-surface in R³ is a point, curve, surface, and solid region respectively. Understanding the M and ∂M are the crucial fact. Because then we can easily decide whether we should go for Curl or Divergence. Like Can you take the Divergence of an open surface? If not, then why?
Now, we can unify all of them by generalized Stokes’ theorem,
Generalized Stokes’ theorem: Suppose M is an oriented surface of dimension n with an (n-1)-dimensional boundary ∂M. if ω is a smooth (n-1)-form on M, then:

Now, we’ll observe how our earlier cases essentially represent the same concept presented in various notations. However, to fully grasp the situation, we require additional tools: Musical isomorphism. I won’t delve deeply into it in this post, but it’s crucial to understand (here I am too sloppy to describe them properly) that a flat (♭) converts a vector into a co-vector, while a sharp (♯) converts a co-vector into a vector. If you understand the isomorphism between V and V^* (dual of V) then you might catch the bigger picture. Take a look at the Wikipedia article.
Suppose we have a vector α,

then applying flat we will get a co-vector,

Similarly, if we have a co-vector ω,

then we can apply sharp on ω and will get a vector,
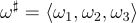
And the final piece is Hodge star ⋆ which convert a k-form to a (n-k)-form. Like,

Then we can see our curl and div can be written using some combination of these operator. Take a vector field V = ⟨V₁,V₂,V₃⟩ then,

Now, if we take exterior derivative we get,

Now apply Hodge star we get,

Finally, turn our co-vector into a vector using sharp operator,

Similarly, we can see the divergence is nothing but,

Now, it’s time to see the left-hand side of the Divergence and Stokes’ theorem through our tools which are nothing but some sort of differential,

And for Green’s theorem it was more straight forward. Because take the differential 1-form ω = Pdx+Qdy then dω become,

Hence,
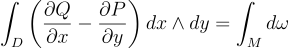
Let’s wrap up here, because it’s 3AM at my local time. If I keep writing, then there will be higher probability I will make more mistake. Let me know if you figure out any mistake or suggestion. We will see how to interpret another sides for each case in the part-2.
